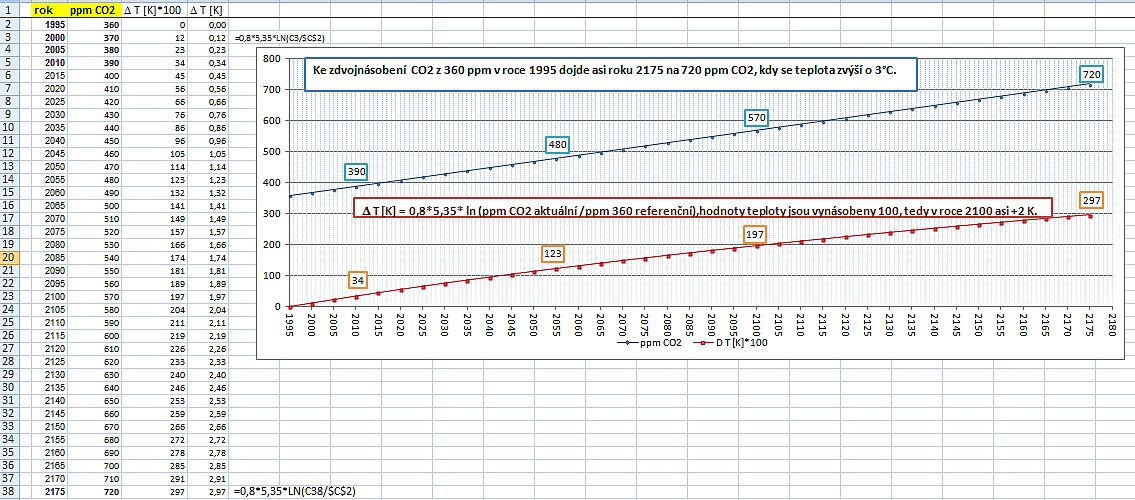
Tato strana v souboru .XLSX ,    CO2-teplota-2100.xlsx
CO2 roste asi 10 ppm za 5 let, tedy od 1995 ( 360 ppm CO2) dosáhne roku 2175 hodnoty dvojnásobku, tedy 720 ppm CO2.
delta F [W/m2] = 5,35*ln( ppm CO2 aktuální/360 ppm referenční)
delta T =0,8* 5,35*ln ( ppm CO2 aktuální/360 ppm referenční)
Do roku 2100 se tedy zvýší teplota o +2°C i se započtením oficiální kladné zpětné vazby ( klimatické citlivosti, forcingu) zahrnující všechno další zvýšení teploty.  Ze Stfan-Boltzmannovy rovnice pímého vyzařování vychází rovnováha mnohem níž, tedy nižší teplota (asi + 1°C, při započtení jakýchsi blíže neurčených vazeb navýšení +3°C). Hybatel tohoto navýšení při zdvojnásobění ppm CO2 z 360 ppm na 720 ppm mi není znám. Zatím se CO2 hromadí v atmosféře, což postihuje vzorec nárůstu polcování IR záření delta F = 5,35*ln( ppm CO2 aktuální/360 ppm referenční). Z emisí 30 mld tun CO2/rok se pohltí do oceánů 2 mld tun/rok, asi 50% tedy 15 mld tun CO2/rok zůstane v atmosféře.
Tento nárůst pohlcování [W/m2] se převede na teplotu koeficientem 0,8.
delta T =0,8* 5,35*ln ( ppm CO2 aktuální/360 ppm referenční)


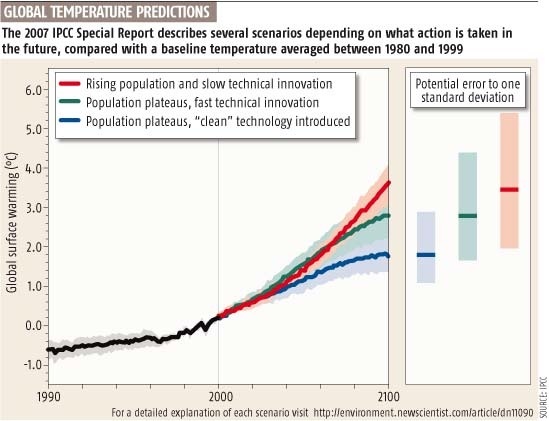
 Podstat problému tedy je v tom, proč IPCC 2007 předpokládá nárůst teploty do 2100 podle dolejšího grafu. Jak lze získat z funkce konkávní odvozené od funkce logaritmus přirozený (ln)
funkci konvexní (červená křivka IPCC 2007) dole? Jedině tím, že předpoklady výpočtů nahoře neplatí. Střední odhad (zelená funkce IPCC 2007) je v doré shodě s hořejším grafem - do roku 2100 bude + 2°C a graf je rovněž konkávní ( typu písmena A).